Timings and Code for Spiking Neural Networks with JAX

 I've been encouraged to flesh out my earlier posts about JAX to support 27DaysOfJAX.

I've written simulations of a Leaky Integrate and Fire Neuron in *Plowman's* (pure) Python, Python + numpy, and Python + JAX.

Here's a plot of a 2000-step simulation for a single neuron:

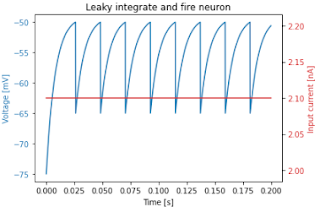Plot for a single neuron

The speedups using Python, Jax and the JAX jit compiler are dramatic.

Pure Python can simulate a single step for a single neuron in roughly 0.25 µs. so 1,000,000 neurons would take about 0.25 seconds.

numpy can simulate a single step for 1,000,000 neurons in 13.7 ms.

Python, JAX + JAX's jit compilation can simulate a single step for 1,000,000 neurons in 75 µs.

Here's the core code for each version.

# Pure Python
def step(v, tr, injected_current):
    spiking = False
    if tr > 0:
        next_v = reset_voltage
        tr = tr - 1
    elif v > threshold:
        next_v = reset_voltage
        tr = int(refactory_period / dt)
        spiking = True
    else:
        dv = ((resting_potential - v) + (injected_current * membrane_resistance)) * (dt / tau_m)
        next_v = v + dv
    return next_v, tr, spiking
    
# numpy
import numpy as np

def initial_state(count):
    potentials = np.full(count, initial_potential)
    ts = np.zeros(count)
    injected_currents = na * (np.array(range(count)) + 1)
    return injected_currents, potentials, ts


def step(v, tr, injected_current):
    rv = np.full_like(v, reset_voltage)
    dv = ((resting_potential - v) + (injected_current * membrane_resistance)) * (dt / tau_m)
    spikes = v > threshold
    next_v = np.where(spikes, rv, v + dv)
    refactory = tr > 0
    next_v = np.where(refactory, rv, next_v)
    next_tr = np.where(refactory, tr - 1, tr)
    R_DUR = int(refactory_period / dt)
    next_tr = np.where(spikes, R_DUR, next_tr)
    return next_v, next_tr, spikes

# JAX (the only difference from numpy is the import)
import jax.numpy as np


def initial_state(count):
    potentials = np.full(count, initial_potential)
    ts = np.zeros(count)
    injected_currents = na * (np.array(range(count)) + 1)
    return injected_currents, potentials, ts


def step(v, tr, injected_current):
    rv = np.full_like(v, reset_voltage)
    dv = ((resting_potential - v) + (injected_current * membrane_resistance)) * (dt / tau_m)
    spikes = v > threshold
    next_v = np.where(spikes, rv, v + dv)
    refactory = tr > 0
    next_v = np.where(refactory, rv, next_v)
    next_tr = np.where(refactory, tr - 1, tr)
    next_tr = np.where(spikes, R_DUR, next_tr)
    return next_v, next_tr, spikes
    
# JAX jitting
from jax import jit

jstep = jit(step)

Jupyter Notebooks containing the full code can be found at https://github.com/romilly/spiking-jax

All the timings were run on an Intel® Core™ i5-10400F CPU @ 2.90GHz with 15.6 GiB of RAM and a NVIDIA GeForce RTX 3060/PCIe/SSE2 running Linux Mint 20.2, JAX 0.2.25 and jaxlib 0.1.73 with CUDA 11 and CUDANN 8.2.

I have successfully run the code on a Jetson Nano 4 Gb.

I've added the Nano timings to the GitHub repository.

Related posts:

Installing JAX on the Nano

More fun with Spiking Neural Networks and JAX

JAX and APL

More updates from @rareblog